

a = a Infinitely many The equation is true for all values of the variable.Ģ 1. x = a One The equation is true for exactly one value of the variable. Inv, lscov, linsolve, and mldivide show significant increase in speed on large double-precision arrays (on order of 10,000 elements or more) when multithreading is enabled.Presentation on theme: "TYPES OF SOLUTIONS OF LINEAR EQUATIONS"- Presentation transcript:Īlgebraic Form Number of Solutions Description a = b None There are no values of the variable for which the equation is true. As a general rule, complicated functions speed up more than simple functions. The operation is not memory-bound processing time is not dominated by memory access time. For example, most functions speed up only when the array contains several thousand elements or more. The data size is large enough so that any advantages of concurrent execution outweigh the time required to partition the data and manage separate execution threads. They should require few sequential operations. These sections must be able to execute with little communication between processes. The function performs operations that easily partition into sections that execute concurrently. For example, with LU decomposition you need to solve two linear systems to solve the original system Ax = b: In practice, however, precomputing the decomposition in this manner can be difficult since you need to know which decomposition to compute (LU, LDL, Cholesky, and so on) as well as how to multiply the factors to solve the problem. The solution to this problem is to precompute the decomposition of A, and then reuse the factors to solve for the different values of b.

However, each subsequent time you solve a similar system of equations with a different b, the operator computes the same decomposition of A, which is a redundant computation. When you solve one of these systems of equations using slash (/) or backslash (\), the operator factorizes the coefficient matrix A and uses this matrix decomposition to compute the solution. However, sometimes the different values of b are not all available at the same time, which means you need to solve several systems of equations consecutively.
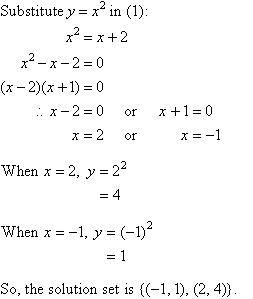
When the different values of b are available at the same time, you can construct b as a matrix with several columns and solve all of the systems of equations at the same time using a single backslash command: X = A\. Some problems are concerned with solving linear systems that have the same coefficient matrix A, but different right-hand sides b. 424/137 Solving for Several Right-Hand Sides


 0 kommentar(er)
0 kommentar(er)
